【Note】Fed-LTD
Fed-LTD:Towards Cross-Platform Ride Hailing via Federated Learning to Dispatch
派单效率受到数据隔离问题(data isolation problem)的影响,本文提出Fed-LTD框架,实现多平台在不共享本地数据的前提下协作派单,提供隐私保护的同时共享派单模型和决策。
挑战:
- 如何最大化跨平台派单的总使用率——高效聚合本地派单决策(二分图)
- 如何在联合派单的情况下实现隐私保护和高效
问题建模
Drivers Set. 司机集合\(U\),\(u\in U\),\(u.loc\) 表示司机的位置
Orders Set. 订单集合\(V\), \(v\in V\),\(v.origin,v.destination,v.reward\) 分别表示订单的出发地、目的地和订单价格
在二分图 \(G=(U\cup V,E)\) 中,边\(e=(e,v)\) 的权重 \(w(u,v)=v.reward\),当\(u.loc\) 和 \(v.origin\) 之间的距离超过一定的阈值\(R\) 后,对应的边会被剪枝
Matching Allocation. \(\mathcal{M}\) 表示一个对二分图 \(G=(U\cup V,E)\) 的派单策略,\((u,v)\) 满足 \(u\in U,v\in V\)且\(u\) 和\(v\)都只在\(\mathcal{M}\)中出现过一次,通过计算派单策略 \(\mathcal{M}\)下的边权和定义使用率函数(utility function) \[ SUM(\mathcal{M}(G))=\sum_{(u,v)\in \mathcal{M}}w(u,v) \] Order Dispatching Problem. 给定batch序列 \(<1,2,...,T>\) , \(t\) 的上一个batch就抵达的订单和司机可以构建当前的二分图 \(G^{(t)}\),目标是找到最佳分配策略 \(\mathcal {M}^{(t)}\) 使得所有batch的使用率和最高 \[ max\sum_{t=1}^TSUM(\mathcal {M}^{(t)}(G^{(t)})) \] 有 \(K\) 个平台\(P_1,P_2,...,P_K\)和一个服务器 \(S\),每个平台 \(P_k\) 有一个本地二分图 \(G_K=(U_k\cup V_k,E_k)\),里面的节点对应该平台的司机和订单
Global Optimum. \(G\) 为全局二分图,全局最优 \(\mu(G)\) 可以理解为在非联邦设置下的最优匹配结果 \[ \mu(G)=\mathop{max}_{<\mathcal{M}^{(t)}>}\sum_{t=1}^TSUM(\mathcal {M}^{(t)}(G^{(t)})) \] Summation of Local Optimum. \(\mu(G_{LS})\) 是本地所有二分图的联合 \[ \mu(G_{LS})=\sum_{k=1}^K\mu(G_k) \] 每个平台的信息共享策略可以被定义为一个子图序列,\(K\) 个平台即 \(<\mathcal{G}_1,...,\mathcal{G}_K>\) ,其中\(\mathcal {G}=\cup _{k=1}^K\mathcal{G}_k\),对于全局最优,\(\mathcal{G}_k=G_k\),对于本地最优的和,\(\mathcal{G}_k=\mathbb {0}\)
Federated Order Dispatching Problem(FOD). 要找到\(G_{Fed}=G_{LS}\cup \mathcal{G}\) 的信息共享策略 \(<\mathcal{G}_1,...,\mathcal{G}_K>\) 使得 \[ \mu(G_{Fed})-\mu(G_{LS})>\Delta \] 目标是使得 \(\Delta\) 尽可能大,在满足隐私限制的前提下,使联合订单分配达到与全局最优相似的表现
算法介绍
本地学习和派单(Local learning and dispatching)
将司机作为agents,司机的地理位置(六边形网格表示)作为states,接单或保持空闲作为actions,价值函数是从某个状态得到的期望累积奖励,即 \(\mathcal{V}(s^{(t)})=\mathbb{E}[\sum_tr^{(t)}|s^{(t)}]\),其中\(s^{(t)}、r^{(t)}\)分别表示batch t内的状态向量和奖励和,价值函数的更新遵循贝尔曼方程,其中,\(\alpha_l、\gamma\) 分别表示学习率和折扣因子。 \[ \mathcal{V}(𝑠^{(t)})\leftarrow\mathcal{V}(𝑠^{(t)})+\alpha_𝑙·\sum_u(r_u^{(t)}+\gamma\mathcal{V}(s_v^{(t+1)})-\mathcal{V}(s_u^{(t)})) \] 每个平台根据已学到的价值做分单决策。将未来奖励的期望通过时间差分误差(TD error)编码为二分图的边权重 \[ w(u,v)=v.reward+\gamma\mathcal{V}(s_v^{(t+1)})-\mathcal{V}(s_u^{(t)}) \]
重建二分图后,采用基于匈牙利方法的二分图最大匹配做本地分配决策。每个平台可以独立地在本地运行,服务器将所有平台的奖励和相加作为baseline(本实验中即LocalSum)
分配模型聚合(Aggregation of Dispatching Models)
随机掩码下的隐私聚合——针对聚合期间的隐私泄露
采用随机掩码(random masking)模糊已升级的网格状态来保护值更新的隐私,\(\Delta \mathcal{V}_k\) 是平台 \(k\) 更新后的价值表,通过下面的掩码方法实现扰乱\(\Delta \mathcal{V}_k\) 的值 \[ \Delta\tilde{\mathcal{V}_k}=\Delta\mathcal{V}_k+\sum_{k'<k}PRG(sd_{k,k'})-\sum_{k'<k}PRG(sd_{k',k}) \] \(PRG(·)\)是一个伪随机生成器,\(sd_{k,k'}\)是一个由平台\(k,k'\) 通过密钥协商算法(key agreement algorithm)生成的随机种子。如下图所示,没有随机掩码的情况下更容易被推断哪个网格被更新了,而随机掩码后敏感信息就难以推断了。
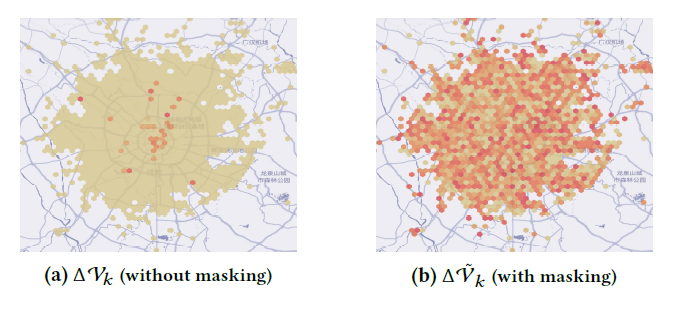
推迟同步——针对服务器和各平台之间的高通讯代价
服务器从每个batch同步一次推迟至每 \(t_d\) 个batches进行一次值同步,将通讯代价减少了\(1/t_d\)
分配决策聚合(Aggregation of Dispatching Decisions)
重建全局二分图
设计基于局部敏感哈希(Locality Sensitive Hashing, LSH)的方法平衡隐私和效率,在哈希后依旧保持了最近邻组合 \[ \text{If } dist(u,v)\le R,\text{ then }Pr[h(u)=h(v)]\ge p_1\\ \text{If } dist(u,v)\ge c·R,\text{ then }Pr[h(u)=h(v)]\le p_2 \] \(dist(·,·)\) 表示欧几里得距离,\(R\) 是连接性阈值(比如3km), \(h\) 是哈希函数
通过LSH编码,可以生成由 \(\mathcal{K}\) 个哈希函数表示的一个节点 \(v\) 的签名 \(Sig(v)=<h_1(v),···,h_{\mathcal{K}}(v)>\),再采用MD5编码哈希函数来保护LSH编码中的相关位置,加密后的签名为\(SSig(v)=MD5(Concat(h(v))\),种子 \(Concat(h(v))\)是 \(\mathcal{K}\) 个二元哈希编码的拼接。编码算法生成要共享的节点的加密签名,服务器通过解码重建二分图。
差分隐私混淆边权
恢复全局二分图结构后,需要计算由强化学习生成的边权。\(v.origin\) 和 \(u.loc\) 相近,根据价值函数的连续性,有 \(\mathcal{V}(v.origin)\approx\mathcal{V}(u.loc)\),那么权重的计算公式可以重写为如下只与订单 \(v\) 有关的公式 \[ w(u,v)\approx v.reward+\gamma\mathcal{V}(v.destination)-\mathcal{V}(v.origin) \] 采用差分隐私来扰动 \(w(u,v)\),服务器就难以通过网格值推断订单和司机的位置。将Laplace噪声加入到边权计算中,敏感度可以通过 \(\Delta _{\mathcal{V}}=\gamma\mathcal{V}_{max}-\mathcal{V}_{min}-(\gamma\mathcal{V}_{min}-\mathcal{V}_{max})=(1+\gamma)diam(\mathcal{V})\) 计算,其中\(diam(\mathcal{V})=\mathcal{V}_{max}-\mathcal{V}_{min}\),那么扰动可以写为 \[ \tilde{w}(v)=w(u,v)+Lap(\frac{(1+\gamma)diam(\mathcal{V})}{\epsilon_p}) \] 其中,\(\epsilon_p\) 为隐私预算(privacy budget)。假设 \(v\) 和 \(v'\) 为两个有同样奖励但任意的起点和目的地,根据Laplace机制,有 \[ \frac{Pr[\tilde{w}(v)=w]}{Pr[\tilde{w}(v')=w]}\le exp(\frac{\epsilon_p}{(1+\gamma)diam(\mathcal{V})}|w(v)-w(v')|)\le e^{\epsilon_p} \] 该公式表示在扰动后难以区分两个订单(\(v\) 和 \(v'\)),服务器难以从边权推断该条边属于哪个订单。每个平台上传经干扰后的边权。最后服务器用贪心算法实现全局匹配,每个平台的司机都可以得到额外的来自其他平台的订单。
算法流程
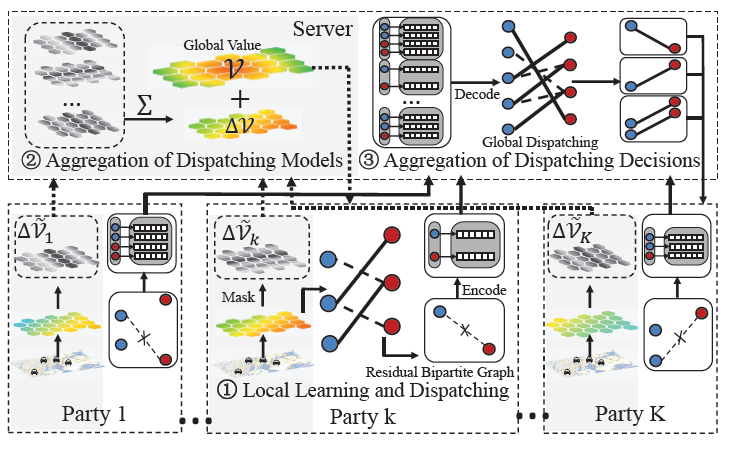
本地学习和派单:每个平台本地学习一个价值函数并基于价值函数做分单决策
聚合分配模型:将联邦学习用于聚合分配模型,同时考虑到隐私保护和效率优化
聚合分配决策:通过聚合本地的残差二分图(每个平台未匹配的节点)共享分配决策