【Note】LTA
Learning to Assign:Towards Fair Task Assignment in Large-Scale Ride Hailing
采用强化学习全面地分配任务,并提出一些加速技巧实现对大规模数据的快速公平的分配。
从司机视角考虑,不公平的分配策略影响司机的感受(the fairness of earnings among drivers)
挑战:
- 在线设置online setting:高维的时空依赖和变化
- 双目标优化bi-objective optimization:在变化的实际限制下同时优化司机的使用率和公平性
- 高效率要求high efficiency requirement:市区数据的快速任务分配
现有的方法的问题:短视,忽略了当前任务分配对未来的影响,缩减了优化空间且降低了利用率和公平性;依赖线性规划或需要多重再分配,在大规模数据上的处理实时响应时效率低下。
衡量指标:
使用率utility——所有司机的收入总和
公平性fairness——一定时间内司机收入的公平性
本文提出的方法中,通过强化学习学习未来感知的任务策略,将使用率和公平性嵌入到同一个增强操作,并利用二分图的稀疏性实现加速;还提出了一个带权的分期偿还的公平性矩阵来刻画更精细时间粒度下司机收入的公平性。
问题建模
将时间 \(T\)分为多个batch \(t\) ,\(W\) 和 \(R\) 分别表示在 \(T\) 内的司机集合和需求集合
Request. 一个订单需求\(r\in R\) 用元组\(<o_r,d_r.p_r,\tau _r>\) 表示,其中 \(o_r,d_r.p_r,\tau _r\)分别表示需求 \(r\) 的出发地、目的地、价格和持续时间
Driver. 一个出租车司机 \(w\in W\) 用元组 \(<l_w^{(t)},u_w^{(t)},a_w^{(t)}>\) 表示,其中\(l_w^{(t)},u_w^{(t)},a_w^{(t)}\)分别表示在 \(t\) 内司机 \(w\) 的当前位置、收入和状态。\(a_w^{(t)}\)为0表示司机处于inactive状态(比如不在线),为1表示司机处于active状态(正在服务一个需求或空闲),假设一个batch内司机的 \(a_w^{(t)}\)不变;若司机在 \(t\) 内处于空闲状态,则收入为零,即 \(u_w^{(t)}=0\),若在 \(t\) 内服务一个需求,则收入为 \(u_w^{(t)}=p_r/\tau _r\)
P.S. 本文考虑到更真实的司机设置依赖,即未来的司机分布会受当前batch内的司机分布和任务分配影响
Bipartite Graph. 候选任务集用二分图 \(G^{(t)}=<R^{(t)},W^{(t)},E^{(t)}>\)表示,其中\(R^{(t)},W^{(t)}\)分别表示 \(t\) 内待分配的订单和空闲司机。若需求 \(r\) 被分配给司机 \(w\),那么就有一条权重为 \(\theta _{r,w}\)的边 \((r,w)\in E^{(t)}\) 连接需求 \(r\) 和司机 \(w\)
另外,需要设置距离上限,当需求-司机的距离小于该阈值时才存在连接两者的边,同时给每条边\((r,w)\)设置一个投影率\(\lambda_{r,w}\) 表示其他用户体验相关的因素。距离阈值和投影率均由平台给出,权重\(\theta_{r,w}\) 初始化为需求 \(r\) 的价格 \(p_r\)
Total Utility. 给定可重用司机集合 \(W\)和动态出现的需求集合 \(R\),总使用率通过所有司机在总时间 \(T\) 内的期望累积收入总和来表示。最大化 \(U\) 来优化所有司机的总收入 \[ U=\sum_{w\in W}\mathbb {E}[\sum_{t\in T}u_w^{(t)}] \] \(M\) 表示一个有利于优化总使用率和收入公平性的匹配策略。司机 \(w\) 的期望累积收入\(\mathbb {E}[\sum_{t\in T}u_w^{(t)}]\)由匹配结果来决定 \[ \mathbb {E}[\sum_{t\in T}u_w^{(t)}]=\sum_{t\in T}\sum_{(r,w)\in M^{(t)}}(1-\lambda_{w,r})·p_r \] Weighted Amortized Fairness. \(F_w\) 是司机 \(w\) 在加权活跃时间内带权分摊的公平性,其中 \(\xi^{(t)}\) 是用于标准化一天内不同时间段潜在收入方差的权重 \[ F_w= \frac {\sum_{t\in T} u_w^{(t)}/\xi^{(t)}}{\sum_{t\in T}a_w^{(t)}} \] Temporal Earnings Fairness. 收入公平性由带权分摊公平度的熵变量来衡量. 大的 \(F\) 表示司机间更为分散的带权分摊公平度,比如不公平的收入分配,所以目标是最小化 \(F\) \[ F=-\sum_{w\in W}log(\frac{F_w}{max_{w\in W'}F_{w'}}) \]
算法介绍
基于学习的Re-weighting
线上学习公式化
司机 \(w\) 在状态\((l_w^{(t)},t)\) 下遵循策略 \(\pi\) 的价值函数\(V_w^{\pi}(l_w^{(t)},t)\) ,通过奖励(rewards)迭代更新价值函数 \[ V_w^{\pi}(l_w^{(t)},t)\leftarrow V_w^{\pi}(l_w^{(t)},t)+\beta·\Delta_w(\forall w\in W) \] \(\beta\)是学习率,\(\Delta_w\) 的定义如下 \[ \Delta_W= \begin{cases} & p_r+V_w^{\pi}(d_r,t+\tau_r)-V_w^{\pi}(l_w,t)\quad \text{if w gets r}\\ & 0 \quad \text{if w is idle} \end{cases} \] 减少状态数量
初始状态数可以表示为 \(N_S \times N_T\) ,空间状态数乘时间状态数,通过以下两种方式减少状态(states)数量:
· 空间价值函数估计。将时空状态空间中的原始价值函数估计为仅考虑空间状态的形式,举例,\(V_w(d_r,t+\tau _r)=V_w(d_r,t)\) 忽略了短暂时间内的状态变化(订单时间一般较短,可以假设不变). 折扣因子 $$ 用于修正对长持续时间的需求的估计的不准确性. 状态数变化:\(N_T ·N_S \rightarrow N_T\) \[ \Delta_W= \begin{cases} & p_r+\gamma ^{\tau _r}V_w(d_r,t)-V_w(l_w)\quad \text{if w gets r} \\ & 0 \quad \text{if w is idle} \end{cases} \] · Agents间的信息共享。 采用合并了所有Agents的价值函数的共享价值函数,更新公式可简化为 \[ V(l)\leftarrow V(l)+\beta'·\sum_{w:l_w^{(t)}\in l}\Delta_w \] 其中 \(\beta'\) 是标准化后的学习率,\(l\) 表示价值函数所有可能的位置
适应不同市区布局
将位置离散化为两层结构并分别平滑不同层的价值函数. 将城市分为六边形/四边形,有多个方向的六边形适合不规则的城市布局,与经纬度平行的四边形适合用于规则区域。按以下方式平滑价值函数 \[ V(l)=\frac{1}{|DIR_H|+|DIR_S|}(\sum_{x\in DIR_H}H(l+x)+\sum_{x\in DIR_S}S(l+x)) \] 其中 \(S\) 和 \(H\) 分别表示六边形和四边形的价值函数,\(DIR_H\) 和 \(DIR_S\) 明确了两层中平滑指向的偏移量.
避免线上学习的冷启动
(Guding) 价值函数初始化为0,导致初始的batch中的任务分配难以考虑到未来情况,需要引导司机提前到合适的区域避免冷启动
双目标任务分配
公平度提升
(Guiding)直接将公平性检查嵌入最大化总使用率的过程。采用KM算法,先找到一条包含连接和未连接的边的道路,若未连接的边权重大于已连接的边的权重,交换两条边提升总使用率;当搜索一条增广路时,检查司机未来的收入率并拒绝有较大收入率方差的增强;为减少检查量和时间消耗,只检查邻接的两个司机间的增强道路。
加速
(Assigning)采用宽度优先搜索(BFS),将二分图分成多个部分,每个部分可能只有一个司机/需求。
算法流程
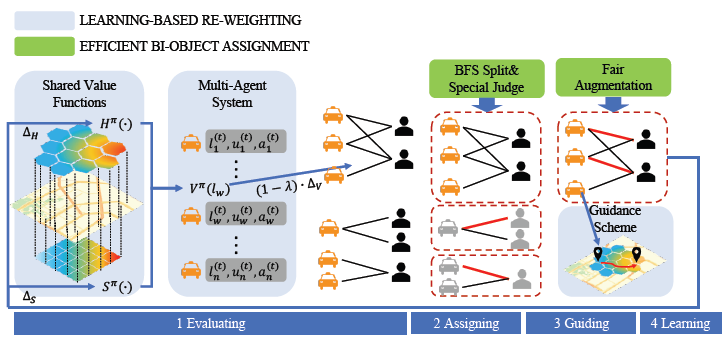
首先re-weighting模块结合跨任务的时间依赖精细化给定二分图的边权重,然后双目标任务模块通过公平性增强和其他加速策略找到分配策略,最后基于学习的re-weighting模块再基于分配结果更新权重,并在某些情况下指引空闲司机到指定区域。