【Note】STGCN

Spatio-Temporal Graph Convolutional Networks:A Deep Learning Framework for Traffic Forecasting

在文中提出的图时空网络STGCN中，定义\(v^t\in\R^n\)为\(n\)个观测点在时间戳\(t\)时的观测向量，\(\mathcal {G}_t=(\mathcal {V}_t,\mathcal {E},W)\)，\(\mathcal {V}_t\)表示顶点(观测点)的集合，\(\mathcal {E}\)表示边的集合，\(W\in \R^{n\times n}\)为\(\mathcal {G}_t\)的邻接权重矩阵。网络的输入为\(M\)个时间步的图的特征向量\(X\in R^{M\times n\times C_i}\)，\(n\)表示观测点的数量，\(C_i\)是数据的特征向量长度，在文中取1，接下来对模型整体架构展开介绍。

空域卷积在每个时间步的图上进行，输入\(X\in R^{n\times C_i}\)，用Chebyshev多项式近似与一阶近似后的图卷积公式，使得在卷积过程中不仅考虑邻居节点的状态，也考虑自身的状态，再对图卷积运算进行泛化。对于完整的时空图(即对应\(M\)个时间步)，其输入为\(X\in\R^{M\times n\times C_i}\)，输出为\(Y\in \R^{M\times n\times C_o}\)

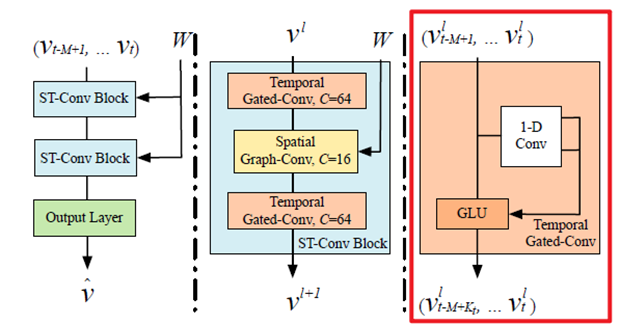
如上图所示，在最右侧的时域卷积块中，每个节点处的输入\(X\in \R^{M\times C_i}\)，沿着时间维度进行一维卷积，时间卷积探索\(K_t\)个输入的邻居每次将序列长度缩短\(K_t-1\)，那么每个有着\(C_i\)个通道的序列长度为\(M\)的节点的输入可以表示为\(Y\in \R^{M\times C_i}\)，卷积核 \(\Gamma \in \R^{K_t\times C_i\times 2C}\)再将\(Y\)映射为独立的输出元素\([P\ Q]\in \R^{(M-K_t+1)\times (2C_O)}\)，分别通过\(GLU\)激活，sigmoid$ 门$\(\sigma(Q)\)控制着当前状态的哪个输入\(P\)与发现时间序列中的组成结构和动态变化相关，非线性门通过堆叠的时间层挖掘输入域。此外，在堆叠的时间卷积层中使用残差连接。同理，可以将卷积核应用于图中的\(n\)个节点，得到最后的输出\(\mathcal{Y}\in \R^{(M-K_t+1)\times n\times C}\)。时间门卷积的公式为\(\Gamma *_\Tau Y=P\odot \sigma(Q)\in \R^{(M-K_t+1)\times C_o}\)。

注：这里对映射输出为单独的P和Q两个元素的方法和原因还不太理解。

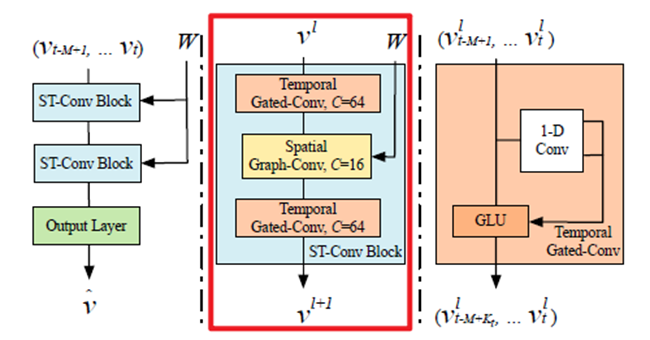
如上图所示，中间的时空卷积块(ST-Conv Block)由两个时域卷积块和一个空域卷积块组成，时空卷积块的输入和输出均为3D张量，对于第 \(l\)个块，输入为\(v^l\in \R^{M\times n\times C^l}\)，输出为\(v^{l+1}\in \R^{(M-2(K_t-1))\times n\times C^{l+1}}\)，计算方式为\(v^{l+1}=\Gamma^l_1*_\mathcal {T}ReLU(\Theta^l*_\mathcal {G}(\Gamma^l_0*_\mathcal {T}v^l))\)，其中\(\Gamma^l_0\)和\(\Gamma^l_1\)分别为时空块\(l\)内上面和下面的卷积核，\(\Theta^l\)是图卷积的谱内核。通过图卷积层对通道进行下缩放和上缩放，实现尺度压缩和特征压缩。

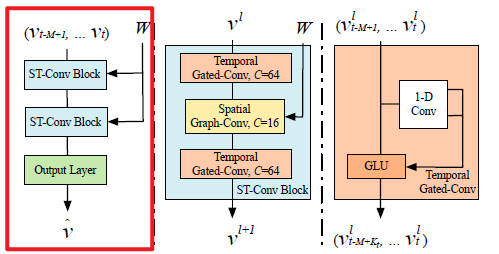
根据时域卷积块的一维卷积，每经过一个时空卷积块，数据在时间维度的长度减小\(2(K_t-1)\)，在叠加两个时空卷积块后，输出\(Y\in\R^{(M-4(K_t-1))\times n\times C_o}\)。输出层包括一个时间卷积层和一个全连接层，时间卷积层把第二个时空卷积块的输出映射为单步预测，得到输出\(Z\in\R^{n\times c}\)，全连接层通过在\(c\)个通道上应用线性变换计算\(n\)个节点在\(t+1\)时间点的预测值\(\hat{v}=Zw+b\)，其中权重参数\(w\in\R^c\)。