【Note】STSGCN

Spatial-Temporal Synchronous Graph Convolutional Networks:A New Framework for Spatial-Temporal Network Data Forecasting

STGCN采用两个分离的模块来捕捉时许和空间的依赖性，只能捕捉节点在同一时间步对邻居节点的影响和对下一时间步的自身的影响，不能直接捕捉节点对下一时间步的邻居节点的影响，而是通过将空间表征喂给时序建模组件来间接捕捉。

提出STSGCN(Network)，直接同步捕捉局部时空关联，构建了能在一张图中关联邻接时间步内独立的空间图的局部时空图，并构建STSGCM (Module)，在局部时空图中捕捉复杂的局部时空关联。设计了STSGCL(Layer)，在不同的时间段部署STSGCM，最后叠加多层来聚合长范围时空关联和异质性用于预测。模型整体架构如下图所示。

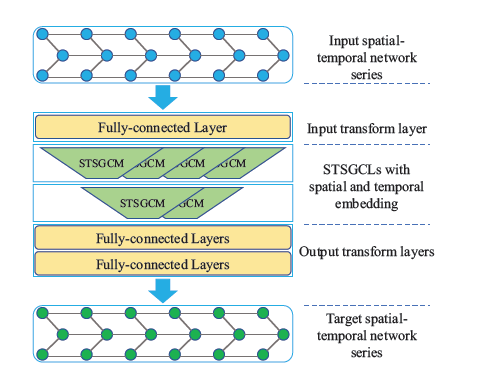
定义空间网络\(\mathcal{G}=(V,E,A)\)，\(V\)表示\(N\)个顶点的集合，\(E\)表示边集合，\(A\)表示网络\(\mathcal {G}\)的邻接矩阵；定义图信号矩阵\(X^{(t)}_\mathcal{G}\in\R^{N\times C}\)表示在时间步\(t\)空间网络\(\mathcal{G}\)的观测情况，\(C\)表示特征的数量。

问题定义，学习函数\(f\)，使得\(f(X^{(t-T+1)}_\mathcal{G},X^{(t-T+2)}_\mathcal{G},...,X^{(t)}_\mathcal{G})=(X^{(t+1)}_\mathcal{G},X^{(t+2)}_\mathcal{G},...,X^{(t+T')}_\mathcal{G})\)

局部时空图构建

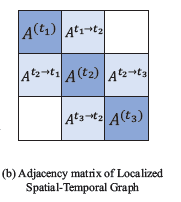
\(A\in\R^{N\times N}\)表示空间图的邻接矩阵，\(A'\in\R^{3N\times 3N}\)表示在三个连续的空间图上构建的局部时空图的邻接矩阵，时间步\(t_1\)上的节点\(i\)在时间步\(t_2\)和\(t_3\)的节点索引分别为\(N+i\)和\(2N+i\)。对角线上表示3个连续时间步空间网络的邻接矩阵，对角线的两侧表示每个节点自身在邻接时间步的连通性。

时空嵌入temporal embedding

在一张图中连接不同时间步中的节点，模糊了每个节点的时间属性。为更好地建模时空关联，在时空网络序列中加入位置嵌入，同时考虑到空间和时间的信息。对时空网络序列\(X_\mathcal{G}\in\R^{N\times C\times T}\)，设计一个可学习的时间嵌入矩阵\(T_{emb}\in\R^{C\times T}\)和空间嵌入矩阵\(S_{emb}\in\R^{N\times C}\)，经训练后包含必要的时空信息。通过广播操作把两个嵌入矩阵加入到时空网络序列中获得网络序列的新的表示：\(X_{\mathcal{G}+t_{emb}+s_{emb}}=X_\mathcal{G}+T_{emb}+S_{emb}\in\R^{N\times C\times T}\).

时空同步图卷积模块STSGCM

图卷积的输入是局部时空图的图信号矩阵，每个节点聚合了自身和邻居节点在邻接时间步的特征，聚合函数是一个线性函数，其权重与节点和其邻居的边的权重相同，然后部署一个带有激活函数的全连接层把节点特征转换到一个新空间，卷积操作可以用公式表示为\(GCN(h^{(l-1)})=h^{(l)}=\sigma(A'h^{(l-1)}W+b)\in\R^{3N\times C'}\)，其中\(A'\in\R^{3N\times 3N}\)，\(h^{(l-1)}\in\R^{3N\times C}\)表示第\(l\)层的输入，可学习参数\(W\in\R^{C\times C'},b\in\R^{C'}\)，激活函数\(\sigma\)为\(GLU\)，控制哪些信息被传递到下一层，图卷积层可以表示为\(h^{(l)}=(A'h^{(l-1)} W_1+b_1)\otimes \mathcal{sigmoid}(A'h^{(l-1)}W_2+b_2)\)，其中可学习参数\(W_1\in\R^{C\times C'},W_2\in\R^{C\times C'},b_1\in\R^{C'},b_2\in\R^{C'}\)。

AGG层包含聚合(aggregating)与裁剪(cropping)两步：聚合采用最大池化层，需要所有输出具有同样的大小，所以一个模块内的图卷积操作的内核数应当相等，聚合操作的公式表示为\(h_{AGG}=max(h^{(1)},h^{(2)},...,h^{(L)})\in\R^{3N\times C_{out}}\)，\(C_{out}\)表示内核数；裁剪用于移除节点在过去和未来时间步的所有特征，去除冗余信息。

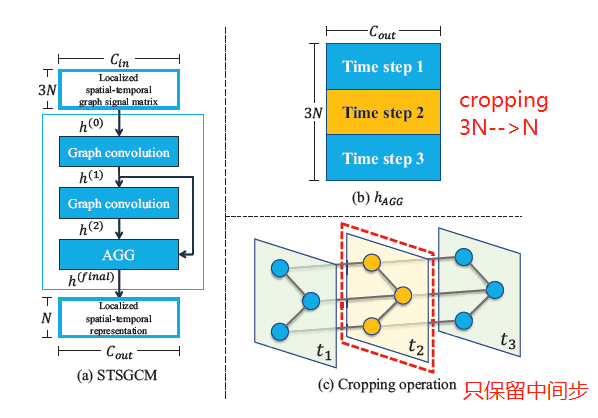
如上图所示，STSGCM的输入为一个局部时空图信号矩阵\(h^{(0)}\in\R^{3N\times C_{in}}\)，经历多个图卷积操作后输出\(h^{(i)}\in\R^{3N\times C_{out}}\)喂给AGG层，先聚合得到\(h_{AGG}\in\R^{3N\times C_{out}}\)，经裁剪后得到最后输出\(h^{(final)}\in\R^{N\times C_{out}}\)。

时空同步图卷积层STSGCL

采用滑动窗口来分不同的时间段，在一个STSGCL中部署多个STSGCMs，各自在不同的时间段上建模局部时空关联，以此捕捉长距时空特征。输入矩阵\(X\in\R^{T\times N\times C}\)，滑动窗口将输入切分成\(T-2\)个时空网络序列\(X\in\R^{3\times N\times C}\)，重塑为\(X'_{reshape}\in\R^{3N\times C}\)直接喂给STSGCM。一层STSGCL部署了\(T-2\)个STSGCMs，他们的输出被拼接成一个矩阵，作为STSGCL的最后输出，公式为\(M=[M_1,M_2,...,M_{T-2}]\in\R^{(T-2)\times N\times C_{out}}\)，\(M_i\in\R^{N\times C_{out}}\)表示第\(i\)个STSGCM的输出。

Mask matrix

增加一个可学习的掩码矩阵\(W_{mask}\in\R^{3N\times 3N}\)，与表示聚合权重的邻接矩阵\(A'\)作点积，得到基于权重调整的局部邻接矩阵\(A'_{adjusted}=W_{mask}\otimes A'\in\R^{3N\times 3N}\)。

Input layer

在最开始设置一个全连接层以转换输入到一个高维空间，提升网络的可表示性。

Output layer

将最后一层STSGCL的输出通过转置和修改输入矩阵的大小，再经过数量为\(T'\)的两个全连接层，最后拼接来得到期望的预测。

Loss function

采用相比均方误差敏感度小一些的Huber loss来计算loss。